대학 2학년 때 AI가 재밌어보여 무작정 찾아간 연구실에서 처음 읽었던 논문을 소개하려 한다. 컴퓨터 비전에도 많은 task가 있지만 Object Detection이나 Image Generation과 달리, Super Resolution은 잘 알려져 있지 않은 듯하다.

Super Resolution에서 Resolution은 해상도, 이미지 안에 몇개의 픽셀이 있는지를 의미하고, 해상도가 높을수록 선명하게 나타난다. Super Resolution은 저해상도 (Low Resolution, LR) 이미지를 고해상도 (High Resolution, HR) 이미지로 바꿔주는 기술을 말한다. 픽셀 수를 늘린다는 점에서 upscaling으로 봐도 무방하다.

문제는 추가되는 픽셀의 RGB 값을 어떻게 계산하여 채울 것이냐다. 방법은 여러가지가 있겠지만, 딥러닝 방식이 시도되기 전까진 sparse-coding 방식이 SOTA로 인정받았다.

Sparse-Coding based Super Resolution

Paper: Image Super-Resolution Via Sparse Representation

아래는 sparse-coding 기반의 Super Resolution을 묘사한 그림이다.

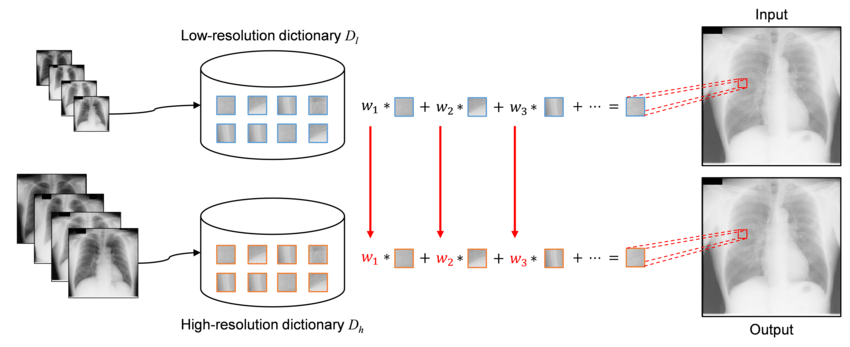
sparse-coding에서는 고해상도 이미지의 패치 $x$와 저해상도 이미지의 패치 $y$가 각각 딕셔너리 $D_h, D_l$의 linear combination으로 계산될 수 있고, linear combination의 계수 $\alpha$는 두 경우가 서로 같다고 가정한다. 식으로 표현하면 아래와 같다.

$$ y = D_l \alpha \\ x = D_h \alpha $$

딕셔너리 $D_h, D_l$는 훈련 데이터의 이미지 패치 쌍들 {$X^h, Y^l$}을 샘플링한 뒤, 식 (1), (2)에 대한 학습을 거쳐 얻을 수 있다. linear combination 결과와 실제 패치 데이터 간의 차이를 최소로 하는 딕셔너리를 구하는 과정이다.

$$ \begin{equation} D_h = \arg\min_{D_h, Z} | X^h - D_hZ |_2^2 + \lambda | Z |_1 \end{equation} $$

$$ \begin{equation} D_l = \arg\min_{D_l, Z} | Y^l - D_lZ |_2^2 + \lambda | Z |_1 \end{equation} $$

linear combination의 계수 $\alpha$는 저해상도 패치 $y$에 대해 식 (3)으로 학습하여 최적 값 $\alpha^*$을 구할 수 있다.

$$ \begin{equation} \alpha^* = \min_{\alpha} | D_l \alpha - y |_2^2 + \lambda | \alpha |_1 \end{equation} $$

따라서 우리는 $D_h, D_l$와 입력 저해상도 이미지가 주어졌을 때, 식 (4)를 계산하여 고해상도 이미지 패치 $x$를 구할 수 있다.

$$ \begin{equation} x = D_h \alpha^* \end{equation} $$

정리하면, 저해상도와 고해상도 이미지 쌍에 대한 학습 데이터가 있을 때, 다음 세 단계를 거쳐 고해상도 이미지로의 변환을 수행할 수 있다.

1. 이미지들을 작은 패치로 나누고, 패치들을 잘 표현하는 다른 공간 (=딕셔너리)을 학습한다.
2. 딕셔너리와 패치 간의 매핑 ($\alpha$)을 학습한다.
3. 고해상도 이미지 패치들을 식 (4)로 구한 뒤, 패치들이 겹쳐지는 곳의 픽셀 값을 계산하여 고해상도 이미지를 완성한다.

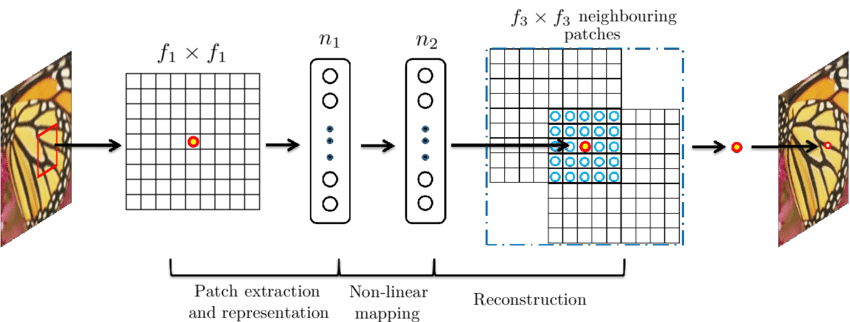
이 sparse-coding 방식의 이미지 복원 성능은 괜찮은 수준이지만, 각각의 입력 패치에 대한 최적의 $\alpha$를 추정하는 데에 많은 연산량이 요구된다. 참조논문에 따르면, bicubic interpolation에 비해 2,000배 이상의 처리시간이 소요된다고 한다.

후술할 딥러닝 기반의 방식들은 그에 비하면 아주 짧은 시간으로도 초해상도 복원 결과를 얻을 수 있다.

SRCNN: SR에 CNN 도입

Paper: Image Super-Resolution Using Deep Convolutional Networks (ECCV 2014)

2012년 AlexNet의 등장으로 CNN이 크게 주목받기 시작하면서, 기존 알고리즘 기반의 이미지 처리 작업을 딥러닝으로 해결하려는 시도들이 이어졌다. Super Resolution (SR) 분야도 예외가 아니었으며, SRCNN(2014)이 최초로 CNN을 활용한 딥러닝 모델로 SR 작업을 수행한 사례다.

sparse-coding 방식에서 살펴보았던 세 단계를 각각 CNN layer로 치환하여 구조적으로도 단순해졌고, 언급하였듯 빠른 시간 안에도 계산이 가능해졌다. 성능상으로도 더 좋은 복원 효과를 입증하였다. 아래는 SRCNN 논문에서 가져온 그림으로, SR 분야의 대표적인 성능 지표 PSNR을 기준으로 SC (sparse-coding)에 비해 더 높은 수치를 기록한 것을 볼 수 있다.

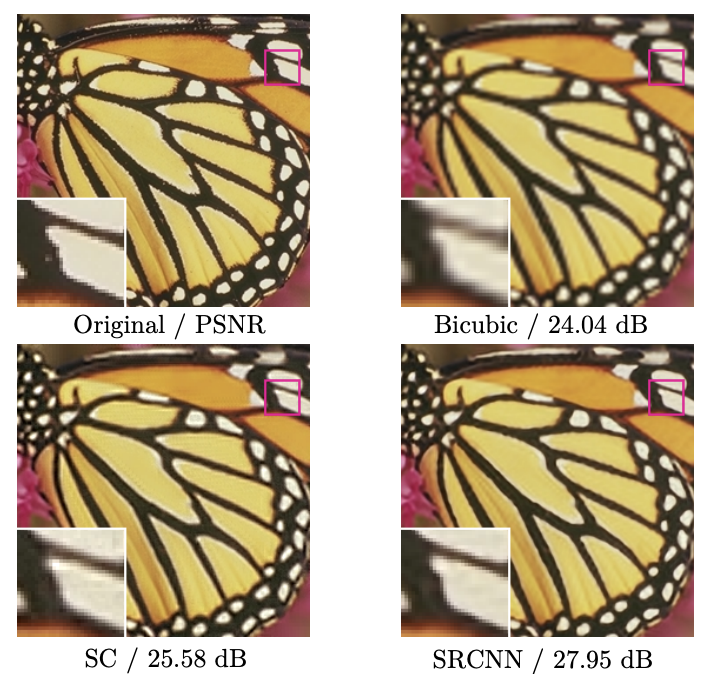
모델의 구체적인 아키텍쳐를 살펴보면 3개의 2D Convolution layer로 구성되어 end-to-end 학습이 가능한 구조이고, 각각의 layer는 sparse-coding에서와 의미상 동일한 기능을 수행한다.

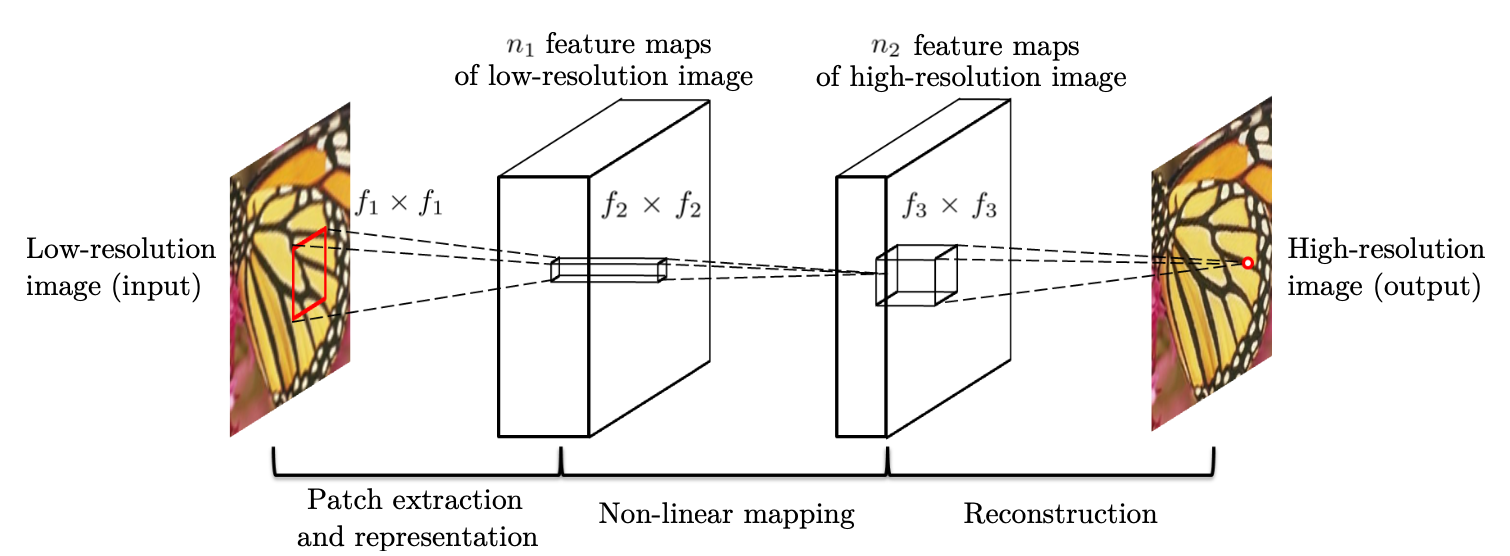
1. Feature extraction layer: Conv2D (9 * 9 size filter, out_channels = 128) + ReLU
   컨볼루션을 수행하면 input에 대한 feature map을 추출할 수 있으므로, sparse-coding의 딕셔너리를 얻는 것과 유사하다.
   

2. Non-linear mapping layer: Conv2D (1 * 1 size filter, out_channels = 64) + ReLU
   1 * 1 크기의 필터를 적용하여 sparse-coding의 linear combination을 재현하려 했다고 한다. 하지만 논문 뒷부분의 실험결과를 보면 3 * 3 또는 5 * 5의 큰 필터를 사용했을 때 더 좋은 결과를 얻을 수 있다.
   

3. Reconstruction layer: Conv2D (5 * 5 size filter, out_channels = 3)
   채널 수가 많은 feature map을 RGB 이미지로 다시 돌려준다. out 채널 수는 RGB 3차원이니 3으로 해도 되고, 구현에 따라 1로 지정하여 학습/추론한 뒤 외부 라이브러리를 통해 RGB 이미지로 바꿔줘도 된다.
   

필터 사이즈가 1보다 큰데 어떻게 upscaling된 이미지를 얻는가 하면, 저해상도 이미지를 먼저 bicubic interpolation으로 원하는 크기의 이미지로 바꾼 뒤, 모델에 넣는다. 논문에 제시된 것과는 다르지만 zero padding을 추가하면 필터 크기에 따른 output 크기 계산도 필요 없어지니, 구현에 참고바란다.

VDSR: Very Deep SR. 깊은 모델로의 도약

Paper: Accurate Image Super-Resolution Using Very Deep Convolutional Networks (CVPR 2016 Oral)

딥러닝이 익숙하지 않은 분들을 위해 잠시 배경설명을 하자면, AlexNet이 주목받았던 ImageNet 챌린지 대회에서 2014년 VGG-Net이 준우승을 거머쥐었다. VGGNet은 모든 Conv의 필터 크기를 비교적 작은 3 * 3으로 고정하여 각 층의 trainable parameter 수를 줄이고, 대신 층을 더 깊게 쌓은 모델이다.

이 방법이 갖는 장점을 예를 들어 설명해보겠다. 3 * 3 conv layer를 3개 쌓는 것과, 7 * 7 conv layer 하나는 receptive field 측면에서 동일한 효과를 갖는다. 하지만 3 * 3 layer 3개의 경우가 더 깊기 때문에 그만큼 activation function을 많이 지나 non-linearity를 많이 가져간다. 게다가 전체적인 parameter 수도 7 * 7 하나의 경우보다 더 적은데, 계산해보면 전자는 3 * 3 * 3 * num_channels, 후자는 7 * 7 * num_channels이다.

픽셀 수를 적게 여러번 줄이기 때문에 계산량이 많고 메모리 측면에서 불리하긴 하지만, 성능이 잘 나올 수밖에 없는 구조이다. 따라서 딥러닝에서는 layer를 깊게, 잘 쌓는 것이 중요하다고 여겨진다.

VDSR 또한 이름에서 알 수 있듯, 필터 사이즈를 줄여 더 깊은 구조로 만든 SR 모델이다. 아래 figure를 보면 SRCNN에 비해 디테일한 부분을 훨씬 잘 복원하는 것을 알 수 있다.

VDSR의 개선사항은 꽤 많고 복잡하니, 여기서부터는 주요 특징점을 나열하는 방식으로 서술할 것이다.

1) 더 넓은 영역의 정보를 사용한다.

9 * 9 크기의 필터도 존재했던 SRCNN과 달리, VGGNet처럼 3 * 3로 고정된 크기의 필터만 사용하여 20 layer를 완성했다.

receptive field의 크기를 계산해보면 41로, 13이었던 SRCNN보다 훨씬 커진 수치이다. output 이미지 픽셀 하나의 값을 예측하는 데에 더 넓은 영역에서의 정보를 사용한다는 의미이므로, 직관적으로도 성능이 크게 증가될 것임을 알 수 있다.

2) residual learning, gradient clipping으로 학습 속도를 높인다.

layer 수가 많으면 back propagation이 시작되는 출력층과 입력층 사이 거리가 멀기 때문에 입력층에 가까운 층들에서 gradient vanishing 현상이 나타난다. 따라서 본 논문에서는 residual learning을 사용하였고, 위 그림에서 마지막에 더해지는 것이 그것이다. 앞 layer에 back propagation의 shortcut을 마련하여 gradient vanishing을 방지한다.

residual learning을 통하면 저해상도 이미지 $x$에 대해 고해상도 이미지 $y$를 직접 예측하는 것이 아닌 residual $r = y - x$를 예측하는 것이기에, 모델에게 더 편한 구조이기도 하다. 따라서 모델의 가중치가 수렴되기까지 더 적은 시간이 걸린다.

loss function도 residual에 대해서만 MSE를 계산하는 방식이다.

$$ \begin{equation} \frac{1}{2} | \mathbf{r} - f(\mathbf{x}) |^2 \end{equation} $$

또한 layer 수가 많기에 본 모델에는 SRCNN에 사용된 learning rate를 그대로 적용하면 학습 속도가 매우 느릴 것이다. 따라서 학습 초기에는 SRCNN보다 $10^4$배 큰 learning rate를 사용하고, 이 경우 발생할 수 있는 gradient exploding을 방지하기 위해 gradient clipping을 적용한다.

물론, 학습이 진행될수록 learning rate를 점점 줄이는 scheduling 기법을 사용한다. 학습코드 참고.

3) 여러 scale (x2, x3, x4)에 적용가능하다.

SRCNN은 하나의 학습된 모델이 하나의 scale factor에 대해서만 SR을 수행할 수 있다고 한다. VDSR은 하나의 저해상도 이미지에 대해 scale이 다른 여러개의 고해상도 이미지 쌍을 두어, 한 모델이 여러 scale에 대한 학습을 동시에 수행할 수 있도록 했다. 단일 scale에 대해서만 학습된 모델보다 일반적인 성능이 우수하다.

⚠️ 구현 시 참고할 점

VDSR의 학습이 수렴하지 않는 경우 또는 가중치 변화가 없는 경우, 가중치 초기화 부분을 확인하기 바란다. He Initialization으로 수정하였더니 학습이 잘 되었다. 논문 저자들의 공식 코드 또는 나의 구현 코드 참고.

마치며

SRCNN과 VDSR이 기존 방식에 비해 많은 발전과 성과를 거뒀음을 보았다. 이 두 모델은 딥러닝 기반의 Super Resolution 연구에서 중요한 초석을 마련한 모델들로, 앞으로 Super Resolution을 연구할 사람이라면 완벽히 이해하고 넘어가면 좋을 것 같다.

다음 포스팅에서는 이후에 등장한 SRGAN, RCAN 등 더욱 발전된 딥러닝 기반 SR 모델들을 살펴보도록 하겠다.